“La ciencia es lo que sabes, la filosofía es lo que no sabes.” ~Bertrand Russell
Bertrand Russell ideó una paradoja muy, pero muy profunda y desconcertante a la vez, al leer y estudiar la lógica del sistema de Gottlob Frege. Frege pensó que él podría definir todos los conceptos matemáticos y probar todas las verdades matemáticas; solo y únicamente con los principios de la lógica. ¿Que Tal?
El que afeita a los barberos, es el que se afeita más o menos?
Tenía Frege también que demostrar la verdad del logicismo, entonces así si habría sido uno de los mayores logros en la historia de la filosofía. Pero su versión del logicismo no fue exitosa.
Uno de los principios lógicos utilizados para demostrar la existencia de números, funciones y otros objetos matemáticos es: por cada **predicado “es F (P)” no es un conjunto de cosas que son F. Dos ejemplos son: “es un número ***primo determina el conjunto de números {2,3,5,7,11 ….} y es una colección determina la colección de todas las colecciones.” En 1903 Russell mostró que (P) es contraria al mismo con el siguiente argumento. Consideremos el predicado “no es un miembro de sí misma.” Con (P) hay una colección ⎯llamarla R⎯ de colecciones que no son miembros de sí mismos. ¿Es R un miembro de sí misma? Si se trata a continuación, no es, y no lo es, entonces es. Una Contradicción! Este fue un golpe devastador a Frege y al logicismo.
Russell escribió que “lo que encierra a todos los miembros de una colección no debe él mismo ser un miembro de una colección” o “la colección de todas las colecciones que son ni miembros de sí mismos es en sí misma, tanto miembro de sí misma y no un miembro de la misma.”
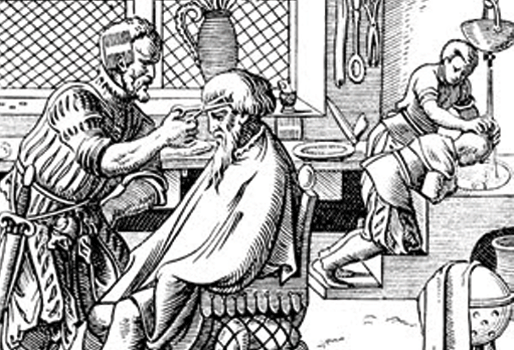
Esto es una paradoja que implica un razonamiento similar al de Russell: “hay un barbero que afeita a todos aquellos y sólo a aquellos que no se afeitan a sí mismos.” Si el barbero se afeita a sí mismo entonces no se afeita a sí mismo. Y si no lo hace entonces el lo hace.
Explicado de otra manera: En mi pueblo soy el único barbero. No puedo afeitar al barbero de mi pueblo, ¡que soy yo!, ya que si lo hago, entonces puedo afeitarme por mí mismo, por lo tanto ¡no debería afeitarme! Pero, si por el contrario no me afeito, entonces algún barbero debería afeitarme, ¡pero yo soy el único barbero de allí!
Esta paradoja es fácil de resolver, al simplemente aceptar que no puede haber tal barbero. Frege no podía aceptar la forma análoga de las colecciones, ya que utilizó su principio para probar la existencia de “colecciones” requeridas por las matemáticas.
*Logicismo: Es la doctrina que sostiene que la matemática es en algún sentido importante reducible a la lógica.
**Predicado: Parte de una proposición que atribuye algo al respecto. Lo que se afirma o afirmado sobre el tema. Por ejemplo, en la proposición, “Sócrates es borracho,” “borracho” es el predicado.
***En matemáticas, un número primo es un número natural mayor que 1 que tiene únicamente dos divisores distintos: él mismo y el 1.
Paradoja: Figura de pensamiento que consiste en emplear expresiones o frases que expresan contradicción.
¿Cuál es la lección?
Lee, piensa y opina…Share.